III-V Calc Info
Introduction
III-V Calc is a software tool for determining III-V semiconductor alloy properties, particular relating to epitaxial thin films used for optoelectronics. Analytical forms are assumed to compute the optical bandgap (direct only) and lattice constant and misfit with respect to a selected substrate, as functions of alloy compositions. Of the six parameters - four compositional parameters, the bandgap, and the lattice constant (misfit) - specifying values for any four parameters restricts the possible values for the other two. For example, if all four composition parameters are specified, the bandgap and lattice constant (misfit) can be determined. Assuming a self-consistent solution does exist, the two restricted parameters can be solved by variational methods. For some choices of the free parameters, either no solution will exist, or the solution may be non-physical.
The composition is specified, using the parameters w, x, y, and z, as:
![]()
In other words:
![]()
An alternative form is:
![]()
where
![]()
The bandgap is evaluated using:
![]()
where the Vegard's-law behavior is:
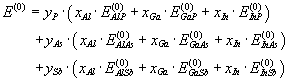
We define the coefficients:
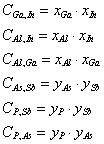 .
.
The bowing contribution due to each pair of sublattice constituents is:
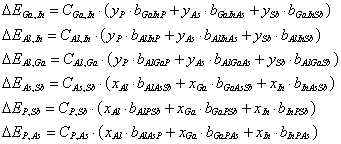
The bowing is taken as a linear combination of sum and average terms:
![]()
where
![]()
as proposed by Moon et al. [1]. Following Adachi [2]:
![]() ,
,
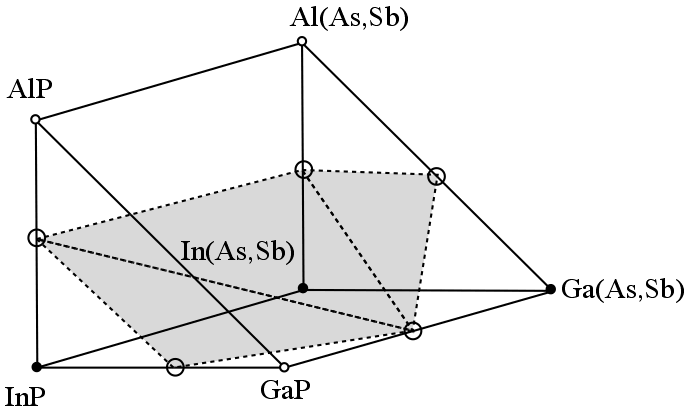
The band type, or alignment, (i.e., direct or indirect) is estimated by modeling the 3-D manifold that divides the 4-D compositional space into direct and indirect subspaces. Coordinates are established as follows:
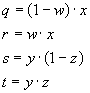
The similarity in transition points for arsenides and antimonides allows mapping the 3-D smanifold onto a 2-D membrane, which can be constructed from triangular segments. The band type at a compositional point can be determined from the numerical sign of the solid angle spanned by the transition surface with respect to that point.
Alloy lattice constants are assumed to obey Vegard's law:
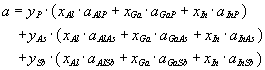 .
.
The misfit is defined as:
![]() ,
,
where a and as are lattice constants for the film and substrate, respectively.
The Marquart-Lavenburg Method is employed in III-V Calc to rapidly converge on a consistent solution, if one exists.
The figure of merit is taken as:
![]() ,
,
where
![]() ,
,
![]() .
.
Where the denominators are reference values
We define a parameter vector
![]() .
.
The variation in F with X is approximately:
![]() .
.
In the plane of two of the variables p and q, the gradient of F is:
![]() ,
,
where the partial derivatives are:
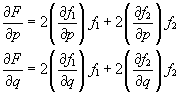 .
.
The gradient vanishes at the minimum. Therefore:
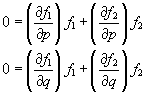 ,
,
or
![]() ,
,
where the Jacobian matrix is:
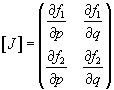 .
.
Considering a small change in coordinates:
![]() ,
,
the Taylor expansion can be used to estimate the changes in the function vector:
![]() .
.
Combining:
![]()
We obtain the system of two equations with two unknowns:
![]() .
.
The increment vector is found by using
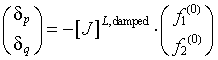
where the damped, left pseudoinverse of the covariance matrix is calculated with a parameter λ to enhance the diagonal terms:
![]()
Increments are computed for λ and λ/n. If F is improved using λ/n, the increments computed using λ/n are accepted, with the change λ→λ/n. If F improves using λ, but not using λ/n, the increments computed using λ are accepted. If neither λ nor λ/n improves F, no increments are accepted and the change is made λ→λ×n. This process is iterated to convergence.
References
1. R. L. Moon, G. A. Antypas, L. W. James, J. Electron. Mat., 3, 635 (1974).
2. S. Adachi, J. Appl. Phys., 53, 8775 (1982).
Acknowledgement
This material is based upon work supported by the Department of Energy-EPSCoR program under Award Number DE-FG02-09ER46503.